欢迎登录
- A. 13
- B. 14
- C. 15
- D. 16
-
解析
本题考查比赛问题。单循环比赛,比赛的场数为
 场,每场比赛胜者得1分、败者得0分,即每场比赛的总分数均为1分。设其余参赛队员得分均为x分,代入选项进行验证:
场,每场比赛胜者得1分、败者得0分,即每场比赛的总分数均为1分。设其余参赛队员得分均为x分,代入选项进行验证:
A选项,n=13,则比赛场数为 =78,总分数为78分,除去甲乙之外还有11人,可列式3+5+11x=78,解得x=
=78,总分数为78分,除去甲乙之外还有11人,可列式3+5+11x=78,解得x= ,不是整数,排除;
,不是整数,排除;
B选项,n=14,则比赛场数为 =91,总分数为91分,除去甲乙之外还有12人,可列式3+5+12x=91,解得x=
=91,总分数为91分,除去甲乙之外还有12人,可列式3+5+12x=91,解得x= ,不是整数,排除;
,不是整数,排除;
C选项,n=15,则比赛场数为 =105,总分数为105分,除去甲乙之外还有13人,可列式3+5+13x=105,解得x=
=105,总分数为105分,除去甲乙之外还有13人,可列式3+5+13x=105,解得x= ,不是整数,排除;
,不是整数,排除;
D选项,n=16,则比赛场数为 =120,总分数为120分,除去甲乙之外还有14人,可列式3+5+14x=120,解得x=8,整数,满足。
=120,总分数为120分,除去甲乙之外还有14人,可列式3+5+14x=120,解得x=8,整数,满足。
故本题选D。 -
拓展
单循环赛制,是指所有参赛队在竞赛中均能相遇一次,n支队伍单循环比赛,场数为
 场。
场。 -
考点
数量关系 数学运算 比赛问题
-
来源
2021年4月3日陕西省西安市(幼小中)统考D类职业能力倾向测验真题第84题
- A. 6
- B. 7
- C. 8
- D. 9
-
解析
第一步,本题考查最值问题中的数列构造。
第二步,35人下班后,剩余上班人数占总人数的40%,则总人数为35÷(75%-40%)=100。此时剩余人数为100×40%=40。每组人数不同且至少3人,要保证尽可能多的分组,则每组人数尽量少,人数分别为3,4,5,6,7,8……,前六组人数加和为3+4+5+6+7+8=33,此时剩余7人不能再单独分组,故最多只能分得6组。
因此,选择A选项。 -
考点
数量关系 数学运算 最值问题
-
来源
模拟题
- A. 25
- B. 26
- C. 27
- D. 28
-
解析
第一步,本题考查最值问题。
第二步,可以先按照“生产部分得的口罩占销售部的3/4,占品质保障部的3/2”来理解,则三个部门分得的口罩之比为:销售部∶生产部∶品质保障部=4∶3∶2,即100箱口罩分成4+3+2=9份,可列式: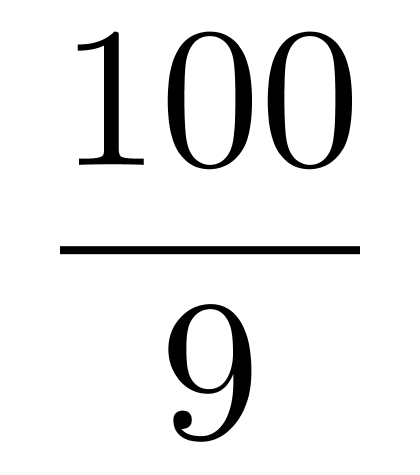 =11……1。分配如下:销售部分得口罩4×11=44箱,生产部分得口罩3×11=33箱,品质保障部分得口罩2×11=22箱,还剩余1箱。要满足题意,这剩余的1箱只能给销售部,此时三部门数量分别为销售部45箱,生产部33箱,品质保障部22箱,此时还不符合“生产部比品质保障部分得的口罩的3/2略多”,需要再把品质保障部拿出一箱给销售部,可得三部门数量分别为销售部46箱,生产部33箱,品质保障部21箱,符合题意。销售部分得的口罩最少比品质保障部分得的口罩多46-21=25箱。
=11……1。分配如下:销售部分得口罩4×11=44箱,生产部分得口罩3×11=33箱,品质保障部分得口罩2×11=22箱,还剩余1箱。要满足题意,这剩余的1箱只能给销售部,此时三部门数量分别为销售部45箱,生产部33箱,品质保障部22箱,此时还不符合“生产部比品质保障部分得的口罩的3/2略多”,需要再把品质保障部拿出一箱给销售部,可得三部门数量分别为销售部46箱,生产部33箱,品质保障部21箱,符合题意。销售部分得的口罩最少比品质保障部分得的口罩多46-21=25箱。
因此,选择A选项。 -
考点
数量关系 数学运算 最值问题,其他最值构造
-
来源
模拟题
- A. 16
- B. 17
- C. 18
- D. 19
-
解析
第一步,本题考查数列构造问题。
第二步,设分得礼物数最少的小朋友分得x个礼物,那么分得礼物数最多的小朋友分得3x个礼物,设分得礼物数第二多的小朋友分得y个礼物,分配情况如下表:
可列方程:3x+y+x+3+x+2+x+1+x=64,解得y=58-7x,且y<3x,那么58-7x<3x,解得x>5.8,那么x最小取6,此时y=16,即分得礼物数第二多的小朋友最多分得16个礼物。
因此,选择A选项。 -
考点
数量关系 数学运算 最值问题,数列构造
-
来源
模拟题
- A. 200
- B. 189
- C. 190
- D. 180
-
解析
由题意可知共有小朋友
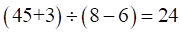 个,则共有糖
个,则共有糖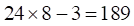 块。故本题选B。
块。故本题选B。 -
考点
中小学专业基础知识 数与代数 奥数,计算题
-
来源
2020年江西省教师公开招聘小学数学笔试试题第17题
- A. 200
- B. 189
- C. 190
- D. 180
-
视频解析
 免费试看
免费试看
-
解析
由题意可知共有小朋友
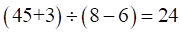 个,则共有糖
个,则共有糖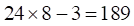 块。故本题选B。
块。故本题选B。 -
考点
中小学专业基础知识 数与代数 奥数,计算题
-
来源
2020年江西省教师公开招聘小学数学笔试真题第17题
- A. 若S继承了B地,则U继承C地
- B. 若S继承了B地,则T继承C地
- C. 若U和V不继承地产,则S和W一定继承了三块地
- D. 若U和V不继承地产,则T和W一定继承了三块地
-
解析
第一步,确定题型。
题干有信息匹配特征,确定为分析推理。
第二步,分析条件,进行推理。
题干信息真假确定,但由于信息众多,可以采用选项代入法。
A项:根据已知条件“若S继承则U不继承”,该项中“若S继承了B地”,则推出U不继承任何土地,该项无法推出,排除;
B项:根据已知条件“若S继承B地则T一定继承D地”,该项中“若S继承了B地”,则推出T继承D地;又因为“C、D两块地不能为同一个人继承”,所以T不能继承C地,该项无法推出,排除;
C项:“若U和V不能继承地产”,则只有S、T、W三人继承。根据已知条件“W继承F而不能继承C”,可得:W继承F地,S或T继承C地;再结合已知条件“继承B地的则不继承其他”,可得:W不能继承B地,S或T继承B地。
如果S继承B地,则T继承C地,根据已知条件“若S继承B地则T一定继承D地”,可得:T继承D地,然而“C、D两块地不能为同一个人继承”,所以假设S继承B地错误。
因此,T继承B地,并且不能继承其它地,那么能够继承3块地的就是S和W。该项说法正确,可以推出。
D项:推理同C项,该项无法推出,排除。
因此,选择C选项。 -
考点
判断推理 逻辑判断 分析推理
-
来源
2016年安徽省(三支一扶)事业单位《职业能力倾向测验》第83题
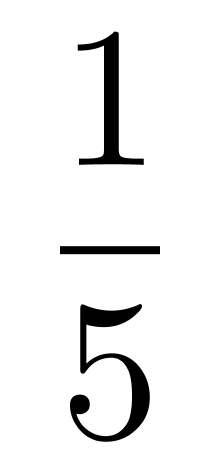 ,且比丙车间的人数少5人,若乙车间分得的人数是最多的,且不超过人数最少车间的3倍,则乙车间最多能分( )人。
,且比丙车间的人数少5人,若乙车间分得的人数是最多的,且不超过人数最少车间的3倍,则乙车间最多能分( )人。 - A. 35
- B. 40
- C. 45
- D. 50
-
解析
第一步,本题考查最值问题中的数列构造。
第二步,根据甲车间分得的人数是其他几个车间的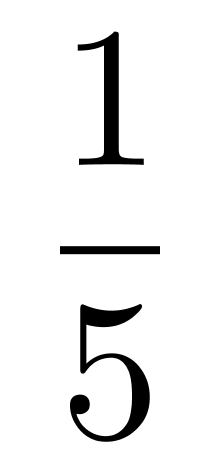 ,设甲车间分得人数为a人,则其他几个车间人数为5a人,可列式a+5a=120,解得a=20,故甲车间分得20人,又根据甲车间比丙车间少5人,故丙车间分得20+5=25人,乙、丁、戊三个车间共分得120-20-25=75人。
,设甲车间分得人数为a人,则其他几个车间人数为5a人,可列式a+5a=120,解得a=20,故甲车间分得20人,又根据甲车间比丙车间少5人,故丙车间分得20+5=25人,乙、丁、戊三个车间共分得120-20-25=75人。
第三步,若甲车间人数最少,为使乙车间分得人数最多,则丁、戊车间人数要尽可能少,即都为20人,此时乙车间人数最多,分得75-40=35人;若甲车间人数不是最少,设乙车间最多分得3x人,则需丁、戊车间人数最少,且都为x人,可列式3x+x+x=75,解得x=15,乙车间最多分得3x=45人。综合两种情况,乙车间最多能分45人。
因此,选择C选项。 -
考点
数量关系 数学运算 最值问题,数列构造
-
来源
模拟题
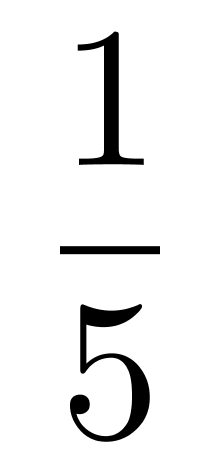 ,且比丙车间的人数少5人,若乙车间分得的人数是最多的,且不超过人数最少车间的3倍,则乙车间最多能分( )人。
,且比丙车间的人数少5人,若乙车间分得的人数是最多的,且不超过人数最少车间的3倍,则乙车间最多能分( )人。 - A. 35
- B. 40
- C. 45
- D. 50
-
解析
第一步,本题考查最值问题中的数列构造。
第二步,根据甲车间分得的人数是其他几个车间的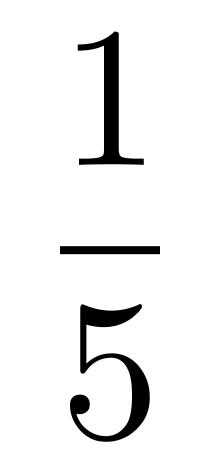 ,设甲车间分得人数为a人,则其他几个车间人数为5a人,可列式a+5a=120,解得a=20,故甲车间分得20人,又根据甲车间比丙车间少5人,故丙车间分得20+5=25人,乙、丁、戊三个车间共分得120-20-25=75人。
,设甲车间分得人数为a人,则其他几个车间人数为5a人,可列式a+5a=120,解得a=20,故甲车间分得20人,又根据甲车间比丙车间少5人,故丙车间分得20+5=25人,乙、丁、戊三个车间共分得120-20-25=75人。
第三步,若甲车间人数最少,为使乙车间分得人数最多,则丁、戊车间人数要尽可能少,即都为20人,此时乙车间人数最多,分得75-40=35人;若甲车间人数不是最少,设乙车间最多分得3x人,则需丁、戊车间人数最少,且都为x人,可列式3x+x+x=75,解得x=15,乙车间最多分得3x=45人。综合两种情况,乙车间最多能分45人。
因此,选择C选项。 -
考点
数量关系 数学运算 最值问题,数列构造
-
来源
模拟题
- A. 按劳分配和按生产要素分配相结合
- B. 按劳分配和按资本要素分配相结合
- C. 按劳分配和按技术要素分配相结合
- D. 按劳分配和按劳动力价格分配相结合
-
解析
第一步,本题考查社会主义市场经济知识。
第二步,小王在国企工作,年薪8万属于按劳分配。股票分得红利和出租房屋是按资本生产要素分配,转让一项技术收入是按技术生产要素分配。
因此,选择A选项。 -
拓展
按劳分配:在公有制经济条件下,按个人提供的劳动数量和质量分配。
按生产要素分配:按投入的生产要素进行收益分配。包括按资本、劳动力、技术、土地等要素进行分配。 -
考点
公基常识 经济 马克思主义政治经济学,社会主义市场经济,社会主义市场经济的基本框架
-
来源
2018年吉林省吉林市事业单位公开招聘考试《通用知识》(考生回忆版)试卷第15题
- A. 28
- B. 33
- C. 35
- D. 38
-
解析
第一步,本题考查最值问题,用最不利构造解题。
第二步,设捐赠的图书总量为y,因为“分给八年级的图书数量是七年级3/2倍”,所以设分给八年级的图书数量为3x,分给七年级的图书数量为2x,则分给九年级的图书数量为y-5x。由“分给九年级的图书数量比三个年级的平均数多60%”,可得方程:y-5x=(1+60%)×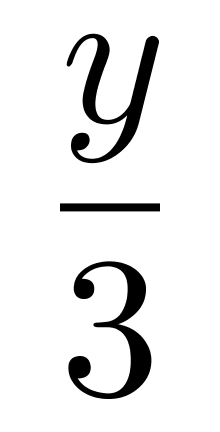 ,化简可得
,化简可得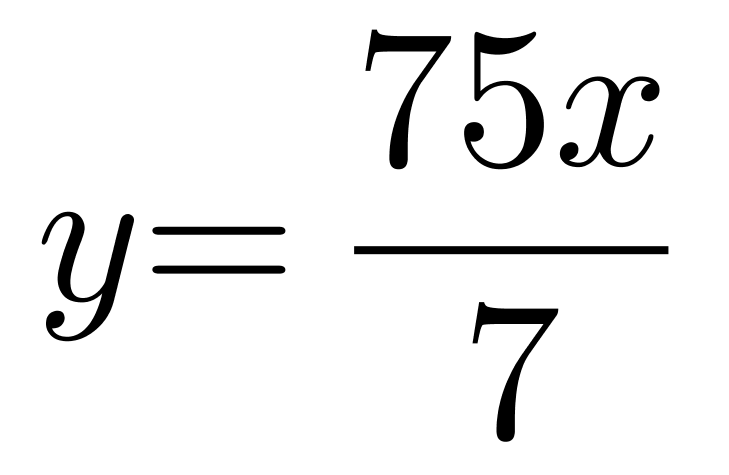 。又因为y的取值范围在400到500之间,则x=42。所以九年级分得图书数量为240。
。又因为y的取值范围在400到500之间,则x=42。所以九年级分得图书数量为240。
第三步,因为要求分得图书数量最多的班级,且题中未说明每班分得图书数量各不相同,则可假设每班人数都为z,则7z=240,解得z约等于34.3,求至少,向上取整,则分得图书数量最多的班级至少分得35本。
因此,选择C选项。 -
考点
数量关系 数学运算 最值问题,最不利构造
-
来源
2022年5月28日黑龙江省大庆市乡村振兴考试试题(精选)(考生回忆版)第65题
- A. 23
- B. 24
- C. 27
- D. 31
-
解析
第一步,本题考查基础应用题问题。
第二步,设单位职工人数为n。则可以得方程:3n+25=4(n-1)+m(m为最后一个人分的数量)。解得n=29-m。又因为0≤m<3,代入可知n可能为27。
因此,选择C选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
2022年6月26日公开招聘“广东兜底民生服务社会工作双百工程”乡镇(街道)社会工作服务站社工笔试考试第20题、2022年6月26日公开招聘“广东兜底民生服务社会工作双百工程”乡镇(街道)社会工作服务站社工笔试考试第75题
- A. 13
- B. 14
- C. 17
- D. 21
-
解析
第一步,本题考查基础应用题,用代入排除法解题。
第二步,优先考虑居中代入,代入B选项,当每个人发三个文件夹时,共有3×14+15=57(个);当每个人发4个时,4×(14-1)=52(个),还剩余57-52=5(个),文件夹剩余较多,人数较少,排除。
代入C选项,当每个人发三个文件夹时,共有3×17+15=66(个);当每个人发4个时,4×(17-1)=64(个),还剩下66-64=2(个),不足3个,符合题意,正确。
因此,选择C选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
2022年7月23日广东省双百工程社工招聘考试第22题、2022年7月23日广东省双百工程社工招聘考试第75题
- A. 7
- B. 9
- C. 13
- D. 23
-
解析
根据已知条件,可得D项正确;根据“余下的大米、面粉和食用盐的袋数之比是1:3:2”可知,余下的大米袋数+余下的食用盐袋数=余下的面粉袋数;假设该村居民有x户,每户分发的大米、面粉和食盐的袋数分别为a、b、c袋,则有:(300-ax)+(163-cx)=(210-bx),化简得:253=(a+c-b)x。因“每户分得的各种物资均为整数袋”,可推知253应该能被x整除,D选项符合题意。A、B、C选项错误。故本题正确答案选D。
-
考点
数量关系 数学运算 基础应用题
-
来源
2016年0124广东江门农信社招聘笔试试题-数资第16题
- A. 7
- B. 9
- C. 13
- D. 23
-
解析
第一步,本题考查余数问题,用代入排除法解题。
第二步,依次代入选项。
A选项:面粉袋数210可以被7整除,没有余数,排除;
B选项:余下大米和面粉之比为3∶3=1∶1,排除;
C选项:余下大米和面粉之比为1∶2,排除。
因此,选择D选项。 -
考点
数量关系 数学运算 余数问题
-
来源
2010年北京公务员考试《行测》试题(社招)第81题
- A. 10000元
- B. 9000元
- C. 6000元
- D. 5000元
-
解析
第一步,本题考查基础公式型经济利润问题,用公式法解题。
第二步,由只收回10000元知,两人共损失25000-10000=15000(元)。根据甲承担 得,乙承担损失15000×(1-
得,乙承担损失15000×(1- )=5000(元),故乙将分得15000-5000=10000(元)。
)=5000(元),故乙将分得15000-5000=10000(元)。
因此,选择A选项。 -
考点
数量关系 数学运算 经济利润问题,基础公式类
-
来源
2012年国家公务员考试《行测》试题第67题
- A. 14
- B. 15
- C. 23
- D. 29
-
解析
设一开始三人每人分得X个五角星,则五角星总数为3X+2,任意两人的五角星数量加起来为2X,根据题意将2X平均分成3份还剩2个,假设其中每一份为m(m为正整数),则有2X=3m+2,联合两式,解得五角星总数为9m/2+5,也就是说五角星总数减5应该是9的倍数,只有14和23符合,所以A、C正确,B、D错误。故本题正确答案选AC。
-
考点
数量关系 数学运算 平均数问题
-
来源
2018年0630贵州农信社招聘笔试试题-数资第87题
- A. 14
- B. 15
- C. 23
- D. 29
-
解析
第一步,本题考查约数倍数问题。
第二步,根据题意平均分给3人还剩2颗,即(总数-2)为3的倍数,排除B选项;代入A选项,每个人分得4个五角星,4×2-2=6也为3的倍数,符合题干所有条件;代入C选项得每个人分得7个五角星,7×2-2=12也为3的倍数,符合题干所有条件;代入D选项得每个人分得9个五角星,9×2-2=16不是3的倍数,不符合题意,排除。
因此,选择A、C选项。 -
考点
数量关系 数学运算 约数倍数问题
-
来源
2017年河北省保定市事业单位《职业能力倾向测验》真题第81题
- A. 10000元
- B. 9000元
- C. 6000元
- D. 5000元
-
解析
第一步,本题考查基础公式型经济利润问题,用公式法解题。
第二步,由只收回10000元知,两人共损失25000-10000=15000(元)。根据甲承担 得,乙承担损失15000×(1-
得,乙承担损失15000×(1- )=5000(元),故乙将分得15000-5000=10000(元)。
)=5000(元),故乙将分得15000-5000=10000(元)。
因此,选择A选项。 -
考点
数量关系 数学运算 经济利润问题,基础公式类
-
来源
2018年0512天津市高校毕业生“三支一扶”考试真题第5题
- A. 14
- B. 15
- C. 23
- D. 29
-
解析
第一步,本题考查约数倍数问题。
第二步,根据题意平均分给3人还剩2颗,即(总数-2)为3的倍数,排除B选项;代入A选项,每个人分得4个五角星,4×2-2=6也为3的倍数,符合题干所有条件;代入C选项得每个人分得7个五角星,7×2-2=12也为3的倍数,符合题干所有条件;代入D选项得每个人分得9个五角星,9×2-2=16不是3的倍数,不符合题意,排除。
因此,选择A、C选项。 -
考点
数量关系 数学运算 约数倍数问题
-
来源
2017年河北省保定市事业单位《职业能力倾向测验》试题(考生回忆版)第81题
联系方式:
咨询优惠
添加您的
专属公考咨询师

有协议班吗?
一课时多长时间?
手机可以观看吗?
课程可以反复学习吗?
可以下载吗?
课程包含图书吗?
错过直播有回放吗?
