(单选题)
对一个边长为1的等边三角形实施如下步骤:
步骤1:沿三边中点的连线,将它分成四个小三角形。
步骤2:去掉中间的那一个小三角形
步骤3:对剩余每个小三角形重复1
操作4次的结果如图,若这样操作5次后,剩余的所有三角形周长和为( )。
A.3
B.729/32
C.243/32
D.729/64
参考答案:B
参考解析:
第一步,本题考查几何问题,可用枚举归纳法。
第二步,观察题干中给出的操作4次的结果图,可发现:
操作1次,剩余的为3个边长为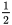 的正三角形;
的正三角形;
操作2次,剩余的为9个边长为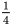 的正三角形;
的正三角形;
操作3次,剩余的为27个边长为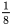 的正三角形;
的正三角形;
操作4次,剩余的为81个边长为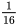 的正三角形;
的正三角形;
故操作5次,剩余的应为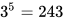 个边长为
个边长为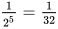 的正三角形,故周长和为
的正三角形,故周长和为 。
。
因此,选择B选项。
知识点:几何问题 数量关系 数学运算 事业单位 职测-联考A类



