(单选题)
在一个棱长为2的正方体上切掉一个角,得到的新的两部分几何体的表面积最大是多少?
A.32+2
B.24+4
C.24+2
D.24+2
参考答案:B
参考解析:
第一步,本题考查几何问题。
第二步,切掉角之后得到的两部分几何体与原正方体相比,多了两个截面的面积。在正方体上切角的最大截面是三个相邻面上的对角线所形成的等边三角形,如下图所示。
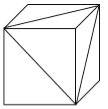
第三步,该三角形的边长为2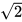 (等腰直角三角形斜边是直角边的
(等腰直角三角形斜边是直角边的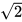 倍),根据等边三角形面积公式S=
倍),根据等边三角形面积公式S=
 可知,该截面的面积为
可知,该截面的面积为 ×
× =2
=2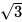 。原正方体的表面积为6×2×2=24,那么两部分的表面积之和为24+4
。原正方体的表面积为6×2×2=24,那么两部分的表面积之和为24+4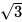 。
。
因此,选择B选项。
知识点:几何问题 数量关系 数学运算 招警 行测



