(单选题)
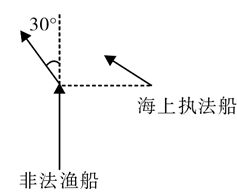
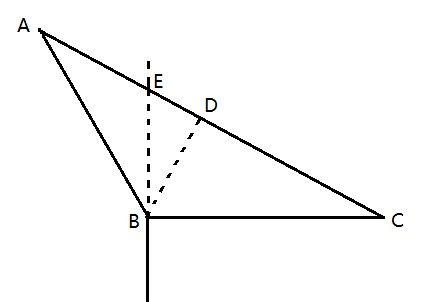
一艘非法渔船作业时发现其正右方有海上执法船，于是沿下图所示方向左转30°后，立即以15节（1节＝1海里/小时）的速度逃跑，同时执法船沿某一直线方向匀速追赶，并正好在某一点追上。已知渔船在被追上前逃跑的距离刚好与其发现执法船时与执法船的距离相同，问执法船的速度为多少节？
A.20
B.30
C.
D.
参考答案：C
参考解析：
第一步，本题考查几何问题，属于平面几何类。
第二步，题干中可知∠ABE＝30°，则∠ABC＝120°，因为渔船逃窜的距离与发现执法船时与执法船的距离相等，即AB＝BC。所以∠A＝∠C＝30°，作BD垂直于AC交AC于D，则AB＝2BD，AC＝2AD＝2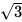
BD，所以AC=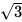AB。由于非法渔船和执法船走AB、AC的时间相同，因此速度之比等于距离之比，可知执法船的速度为15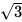海里/小时。
因此，选择C选项。
知识点：几何问题 数量关系 数学运算 地市级公务员考试 地级市考
返回顶部