(单选题)
有一个三棱锥,每个面均为边长为2的正三角形,已知该三棱锥的四个顶点位于同一个球面上,则此球的体积为:
A.2π
B.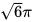
C.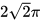
D.3π
参考答案:B
参考解析:
第一步,本题考查几何问题,属于立体几何类。
第二步,由于三棱锥的边长均为2,故可借助正方体辅助求解,构造棱长为 的正方体,如下图:
的正方体,如下图:
B1-ACD1是棱长为2的正四面体,且正四面体B1-ACD1与正方体ABCD-A1B1C1D1有相同的外接球,设外接球的半径为r,则外接球的直径为正方体的对角线即2r= ,r=
,r= 。所以此球的体积V球=
。所以此球的体积V球= 。
。
因此,选择B选项。
知识点:几何问题 数量关系 数学运算 地市级公务员考试 地级市考



