(单选题)
一个正方形跑道边长为20米,甲和乙从跑道上的不同位置同时出发,匀速沿逆时针跑步,已知两人出发的位置之间直线距离为20米,甲以2米/秒的速度跑6秒到达某个顶点后,又跑了不到10秒正好到达乙出发的位置,此时乙正好第二次跑到顶点位置。问以下哪个描述是正确的?( )
A.甲出发后不到2分钟第一次追上乙
B.甲出发后超过2分钟第一次追上乙
C.乙出发后不到2分钟第一次追上甲
D.乙出发后超过2分钟第一次追上甲
参考答案:A
参考解析:
本题属于行程问题。
由甲以2米/秒的速度跑6秒到达某个顶点,画出图示。如图所示: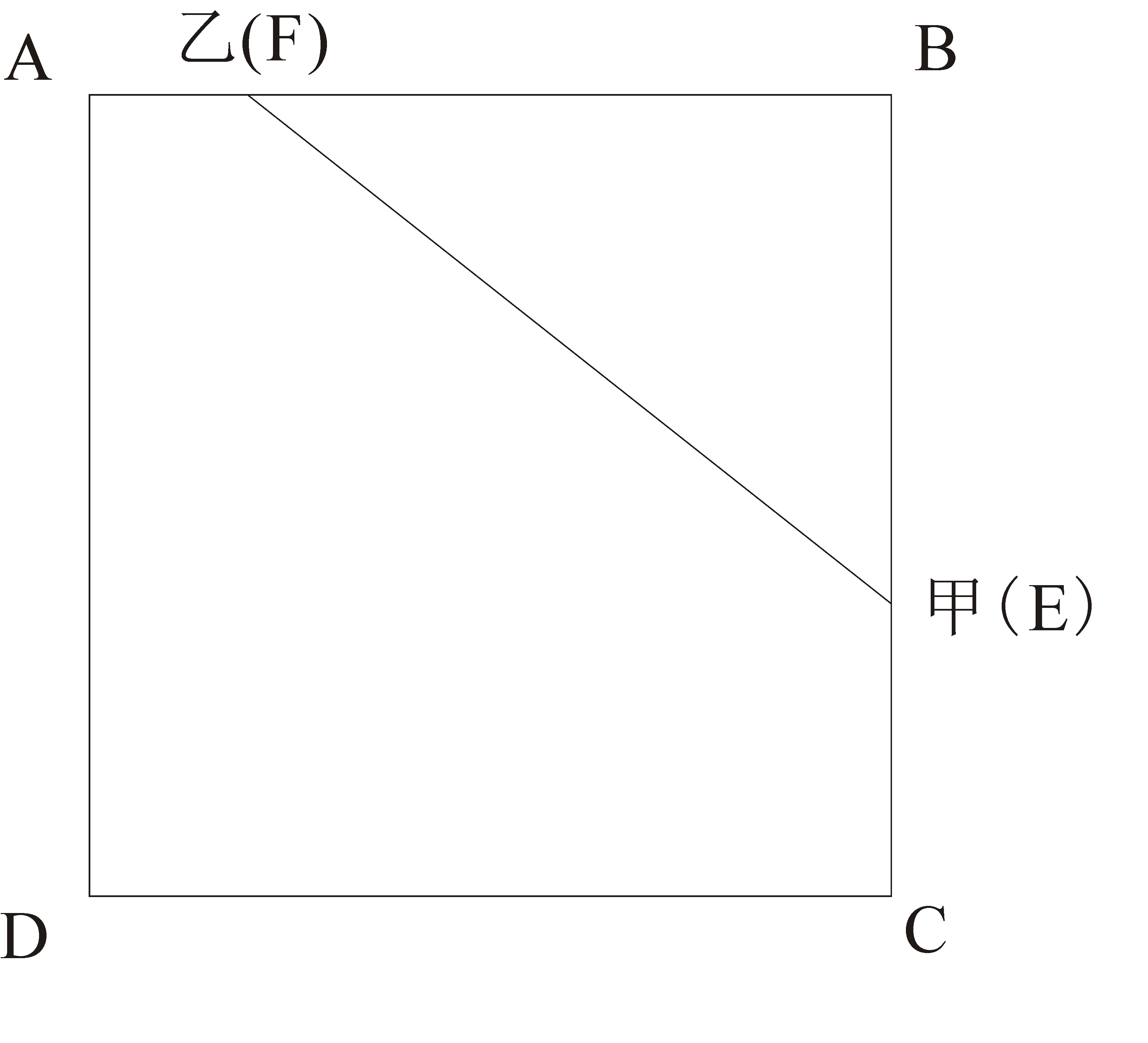
甲初始位置在E点,EB=6×2=12米,由题意又跑了不到10秒正好到达乙出发的位置,所以画出示意图乙出发点在F点,且EF=20。由勾股定理可求得BF=16。甲到达乙的出发点共用时(12+16)÷2=14秒。又因为此时乙正好第二次跑到顶点位置,即跑到了D点,所以乙的速度为(4+20)÷14=12/7。甲的速度大于乙的速度,所以甲出发后,追上乙需要的时间为(12+16)÷(2-12/7)=98s。A符合题意。
因此,选择A选项。
知识点:数学运算 行政能力测验 数量关系 金融业务 模考估分



