(单选题)
某市共有5个县,其位置如图所示,现用红、黄、绿、蓝4种颜色给地图上色,要求任意相邻的两个县的颜色不同,问共有多少种不同的上色方法?
A.32
B.64
C.96
D.144
参考答案:C
参考解析:
解法一:
第一步,本题考查排列组合问题,属于基础排列组合。
第二步,从相邻最少的入手,所以先涂E,4种颜色选一种,有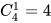 (种)涂法;再涂与E相邻的B、D,用除去涂E的颜色、剩余的3种颜色中的两种颜色涂,有
(种)涂法;再涂与E相邻的B、D,用除去涂E的颜色、剩余的3种颜色中的两种颜色涂,有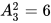 (种)涂法;再涂与B、D都相邻的A,除去涂B、D的两种颜色、用剩余的2种颜色中的一种,有
(种)涂法;再涂与B、D都相邻的A,除去涂B、D的两种颜色、用剩余的2种颜色中的一种,有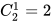 (种)涂法;最后涂C,除去涂A、D的两种颜色、用剩余的2种颜色中的一种,有
(种)涂法;最后涂C,除去涂A、D的两种颜色、用剩余的2种颜色中的一种,有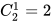 (种)涂法。分步用乘法,总共有4×6×2×2=96(种)。(或先涂C,则顺序为:C→A、D→B→E,计算是一样的)
(种)涂法。分步用乘法,总共有4×6×2×2=96(种)。(或先涂C,则顺序为:C→A、D→B→E,计算是一样的)
因此,选择C选项。
解法二:
第一步,本题考查排列组合问题,属于基础排列组合。
第二步,第一种情况,A、E颜色相同:①B、C颜色相同,则有 (种)涂法;②B、C颜色不同,则有
(种)涂法;②B、C颜色不同,则有 (种);第二种情况,A、E颜色不同:①B、C颜色相同,则有
(种);第二种情况,A、E颜色不同:①B、C颜色相同,则有 (种);②B、C颜色不同,因为A与B、D、C都相邻,则其颜色一定不相同,E与B、D相邻,与C不相邻,则E与B、D不相同,与C可以相同,又因为B、C颜色不相同,则E一定与C相同,则有
(种);②B、C颜色不同,因为A与B、D、C都相邻,则其颜色一定不相同,E与B、D相邻,与C不相邻,则E与B、D不相同,与C可以相同,又因为B、C颜色不相同,则E一定与C相同,则有 (种)。分类用加法,总共有24+24+24+24=96(种)。因此,选择C选项。
(种)。分类用加法,总共有24+24+24+24=96(种)。因此,选择C选项。
知识点:



