(单选题)
上午8点8分,东东骑自行车从家出发,8分钟后,爸爸骑摩托车去追他,在离家4千米的地方追上东东,然后爸爸立即回家,回到家后又马上回头去追东东,再追上东东时,恰好离家8千米,这时是:
A.8点24分
B.8点32分
C.8点48分
D.8点56分
参考答案:B
参考解析:
解法一:
第一步,本题考查行程问题,属于相遇追及类。
第二步,根据题意画图: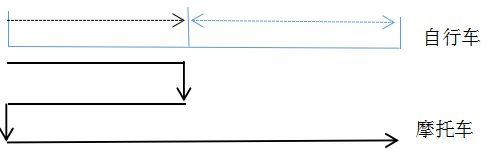
从爸爸第一次追上东东到第二次追上这一段时间内,东东走的路程是8-4=4(千米),而爸爸行了4+8=12(千米),因此,摩托车与自行车的速度比是12∶4=3∶1。东东全程骑车行8千米,爸爸来回总共行4+12=16(千米),还因晚出发而少用8分钟,从上面算出的速度比得知,东东骑车行8千米,爸爸如同时出发应该骑24千米,现在少用8分钟,少骑24-16=8(千米),因此推算出摩托车的速度是每分钟1千米。爸爸总共骑了16千米追上东东,需16分钟,此时东东走了8+16=24(分钟),所以此时是8点32分。
因此,选择B选项。
解法二:
第一步,本题考查行程问题,属于相遇追及类。
第二步,从爸爸第一次追上东东到第二次追上这一段时间内,东东走的路程是8-4=4(千米),而爸爸行了4+8=12(千米),因此,摩托车与自行车的速度比是12∶4=3∶1,即东东的速度是爸爸速度的 。爸爸从家到第一次追上东东,东东走了4千米,若爸爸与东东同时出发,则爸爸应走出12千米,但是由于爸爸晚出发8分钟,所以只走了4千米,所以爸爸8分钟应走8千米。由于爸爸从出发到第二次追上东东共走了16千米,所以爸爸用了16分钟,此时离东东出发共用了8+16=24(分钟),所以爸爸第二次追上东东时是8点32分。
。爸爸从家到第一次追上东东,东东走了4千米,若爸爸与东东同时出发,则爸爸应走出12千米,但是由于爸爸晚出发8分钟,所以只走了4千米,所以爸爸8分钟应走8千米。由于爸爸从出发到第二次追上东东共走了16千米,所以爸爸用了16分钟,此时离东东出发共用了8+16=24(分钟),所以爸爸第二次追上东东时是8点32分。
因此,选择B选项。
解法三:
第一步,本题考查行程问题,属于相遇追及类,用方程法解题。
第二步,设东东速度为x,爸爸速度为y,根据题意列式: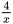 =
=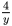 +8①、
+8①、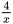 =
=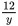 ②,联立等式解得,x=
②,联立等式解得,x= 、y=
、y=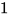 。东东整个过程行走8千米,用时8÷
。东东整个过程行走8千米,用时8÷ =24(分钟),所以这时的时间为8点8分+24分=8点32分。
=24(分钟),所以这时的时间为8点8分+24分=8点32分。
因此,选择B选项。



