(单选题)
某美术培训机构开设了素描、国画、油画三个儿童兴趣班,每名儿童最多可以参加两个(可以不参加)。那么,至少有( )名儿童,才能保证有不少于5名儿童参加兴趣班的情况完全相同。
A.27
B.28
C.29
D.30
参考答案:C
参考解析:
解法一:
第一步,本题考查最值问题,属于最不利构造。
第二步,由“至少……才能保证”,可知此题属于最不利构造问题,答案为最不利情况+1。由“每名儿童最多可以参加两个(可以不参加)”,可得参加方式有以下三种情况:(1)都不参加:1种;(2)只参加一个兴趣班: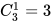 (种);(3)参加其中两个兴趣班:
(种);(3)参加其中两个兴趣班: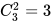 (种)。根据排列组合分类原则,可得参加方式共有1+3+3=7(种)。要求至少有5名儿童参加情况完全相同,最不利的情况为每种参加方式各有4人,共4×7=28(人)。故至少要有28+1=29(个)儿童,才能保证有不少于5名儿童参加兴趣班的情况完全相同。
(种)。根据排列组合分类原则,可得参加方式共有1+3+3=7(种)。要求至少有5名儿童参加情况完全相同,最不利的情况为每种参加方式各有4人,共4×7=28(人)。故至少要有28+1=29(个)儿童,才能保证有不少于5名儿童参加兴趣班的情况完全相同。
因此,选择C选项。
解法二:
第一步,本题考查最值问题,属于最不利构造,用代入排除法解题。
第二步,由“至少……才能保证”,可知此题属于最不利构造问题,答案为最不利情况+1。“保证有不少于5名儿童参加兴趣班的情况完全相同”,最不利的情况为每种参加方式各有4人,设每个儿童有x种报名方式,至少需要的儿童数为y人,可得方程y=4x+1,利用“y-1是4的倍数”代入选项,只有C选项满足。
因此,选择C选项。
知识点:



