(单选题)
如下图所示,在边长为1米的正方形ABCD中,AC与BD相交于O,分别以正方形的四个顶点为圆心,以对角线长度的一半为半径画圆弧与正方形的边相交,则图中阴影部分的面积为多少平方米?(π=3.14)
A.0.43
B.0.57
C.0.79
D.0.86
参考答案:B
参考解析:
第一步,本题考查几何问题,属于平面几何类。
第二步,如下图所示,粗线阴影部分为四分之一圆减去一个正方形,总阴影为四个上图的粗线阴影部分,所以总阴影面积为大圆减去正方形ABCD。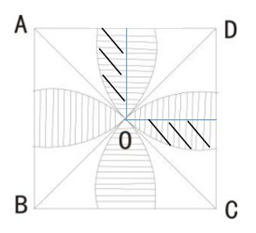
第三步,圆的半径为OD,在等腰直角三角形COD中,斜边是直角边的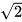 倍,则OD=
倍,则OD= =
=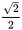 ,阴影部分的面积=圆的面积-正方形ABCD的面积=π(
,阴影部分的面积=圆的面积-正方形ABCD的面积=π(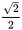 )²-1=
)²-1= -1=0.57(平方米)。
-1=0.57(平方米)。
因此,选择B选项。
知识点:几何问题 数量关系 数学运算 事业单位 职测-联考C类



