要建造一个容积为8立方米，深为2米的长方体无盖水池，如果池底和池壁的造价分别为每平方米120元和80元，那么水池的最低造价为多少元?

参考解析：

解法一：
第一步，本题考查几何问题，属于立体几何类，用方程法解题。
第二步，容积为8立方米，深为2米，那么池底的面积为8÷2＝4（平方米），池底的造价＝单价×面积＝120×4＝480（元）。
第三步，池底的面积为4平方米，设其中一条底边长为x，则另一底边长为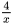 。池底的周长为 2，池壁的造价＝周长×高×单价＝2 ，根据均值不等式可知当 时总价最低，即x＝2（米），此时池壁的造价为320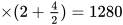 （元）。
第四步，总造价＝池底造价＋池壁造价＝480＋1280＝1760（元）。
因此，选择A选项。
解法二：
第一步，本题考查几何问题，属于立体几何类。
第二步，总容积即总体积为8，则底面积为8÷2＝4（平方米）。池底造价一定，总价最低则池壁面积最小。池壁面积＝底面周长×深度，由几何性质（平面图形中，面积一定时，越接近于圆，周长越小）可知，当底面是正方形时池底周长最小，此时池底边长为2米，周长为8米，池壁面积＝8×2＝16（平方米），池壁造价为16×80＝1280（元），池底造价为4×120＝480（元），总价为1280＋480＝1760（元）。
因此，选择A选项。