(单选题)
在边长为1的正方体ABCD—A1B1C1D1中，点P为面BCC1B1的中心，则三棱锥P-ACD1的体积＝？
A.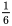
B.
C.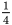
D.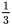
参考答案：A
参考解析：
第一步，本题考查几何问题，属于立体几何类。
第二步，因为ABCD—A1B1C1D1是正方体，所以|AC|²=|AB|²+|BC|²=2、|CP|²=
×(|BC|²+|BB1|²)=
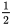、|AP|²=(|AB|²+|BP|²)=
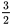；于是，|AC|²=(|AP|²+|CP|²)，即AP⊥CP；同理可证，D1P⊥CP，那么CP⊥面AD1P，从而V(P-ACD1)=V(C-AD1P)=
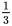×S(△AD1P)×|PC|。
第三步，S(△AD1P)=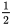×S(▱ABC1D1)=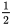×|AB|×|BC1|=
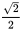，所以V(P-ACD1)=V(C-AD1P)=
。
因此，选择A选项。
知识点：几何问题 数量关系 数学运算 事业单位 职测-非联考
返回顶部