2017年政法干警考试已经进入备考状态，建议各位考生可以根据自身情况，做出合理考试安排。本文华图网校分享2017年政法干警考试行测备考：必考点之比赛问题，以便同学们可以更好地进行备考。

　　2017年政法干警考试行测备考：必考点之比赛问题

　　政法干警考试中“比赛问题”一般涉及循坏赛、淘汰赛、计分、场次、胜负等概念，是一种非常灵活的考试题型。

　　循坏赛：N支队伍进行循坏赛，每支队伍和其他任意队伍都需要进行一场比赛，所以每支队伍需要进行(N-1)场比赛;由于每场比赛都是2个队伍共同进行，所以总场次应该为

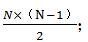
　　淘汰赛：每场比赛淘汰一支队伍，每轮比赛淘汰一半的队伍(如果总数不是偶数，比如一共13支队伍，那么淘汰6支，留下7支队伍)。

　　【例1】某高校学生处要在大一新生中组织篮球比赛，赛制为单循环形式，即每两队都赛一场，如果学生处计划安排36场比赛，则应邀请多少支球队参加比赛?( )

　　A.5 B.8 C.7 D.6

　　【答案】C

　　【解析】假设参加比赛的球队有N支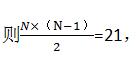，所以N=7。

　　【例2】某羽毛球赛共有23支队伍报名参赛，赛事安排23支队伍抽签两两争夺下一轮的出线权,没有抽到对手的队伍轮空，直接进入下一轮。那么，本次羽毛球赛最后共会遇到多少次轮空的情况?( )

　　A.1 B.2 C.3 D.4

　　【答案】B

　　【解析】淘汰赛，每轮淘汰一半的队伍，第一轮23支，有1支轮空1次，第二轮有12支队伍轮空0次，第三轮有6支队伍轮空0次，第四轮有3支队伍有1支轮空1次，第五轮2支队伍轮空0次，所以总共会遇到1+1=2(次)。

　　【例3】某单位五个科室间举办拔河比赛，每两个科室之间最多比赛一场。其中甲、乙、丙、丁科室分别参加了4、3、2和1场比赛，问已经进行了多少场比赛?( )

　　A.8 B.7 C.6 D.5

　　【答案】C

　　【解析】如图所示，前四个科室分别参加了4、3、2、1场比赛：

　　1.甲赛过4场，所以他与其他4个科室都有连线;

　　2.丁赛过1场，而甲与之赛过，所以丁跟其余3个科室都没有赛过;

　　3.乙赛过3场，但丁没有与之赛过，所以乙跟其余3个科室都赛过;

　　4.丙赛过2场，而甲、乙都与之赛过，所以丙跟其余2个科室都没有赛过;

　　如此连线下来，图中共有6根连线，总共进行了6场比赛。

　　以上就是华图网校分享的2017年政法干警考试行测备考：必考点之比赛问题，希望对大家有所帮助，备考绝不是一蹴而成的事情。希望考生们都可以耐下心来，取得一个满意的成绩!

添加您的专属公考咨询师

扫码免费领取专属学习礼包

领取资料 咨询优惠