(单选题)
有一种装白酒的瓶身为圆柱形，容积为580毫升。正放时白酒高12厘米，倒放时空余部分的高为3厘米。则瓶内现有白酒（ ）毫升。
A.464
B.386
C.483
D.543
参考答案：A
参考解析：
解法一：
第一步，本题考查几何问题，属于立体几何类。
第二步， 由于白酒的瓶身为圆柱形，因此正放和倒放，白酒的高度都是一样的，根据“正放时白酒高12㎝,倒放时空余部分的高为3㎝”，可得瓶身的高度为15㎝，根据圆柱形体积公式可得圆柱形的底面积为：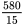
平方厘米，则白酒的体积为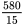： ×12＝464（立方厘米），也就是464毫升。
因此，选择A选项。
解法二：
第一步，本题考查几何问题，属于立体几何类。
第二步，设瓶中白酒的体积为
，空气的体积为
，酒瓶的底面积为S。正放时白酒体积＝S×12，倒放时瓶中空气的体积＝S×3，由此可知∶＝12∶3＝4∶1，故白酒的体积＝580×
＝464（毫升）。
因此，选择A选项。
知识点：几何问题 数量关系 数学运算 事业单位 职测-联考C类
返回顶部