(单选题)
甲班有40名学生,在一次满分为100分的考试中,全班的平均成绩为85分,则成绩低于60分的学生最多有( )人。
A.11
B.12
C.13
D.14
参考答案:D
参考解析:
解法一:
第一步,本题考查最值问题,属于其他最值构造,用十字交叉法解题。
第二步,由“全班平均成绩为85分”可知,每人丢分情况为15分;全班40个学生,共丢分40×15=600(分)。要想60分以下的人尽可能多,则高于平均分的那一部分人不丢分,即每人100分;每个低于60分的人丢分高于40分,总丢分一定,每个人丢分越少,则这一部分总人数越多,则每人按丢分41分来算,即每人得分59分,则根据十字交叉法可得: 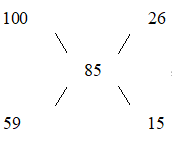 ,则得100分人数/得59分人数=
,则得100分人数/得59分人数=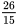 ,总人数40人,则低于60分的人数即得59分的人数为
,总人数40人,则低于60分的人数即得59分的人数为 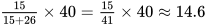 ,因此取整最大值应为14。
,因此取整最大值应为14。
因此,选择D选项。
解法二:
第一步,本题考查最值问题,属于其他最值构造,用极值思想解题。
第二步,由“全班平均成绩为85分”可知,每人丢分情况为15分;全班40个学生,共丢分40×15=600分,要想求低于60分人数的最大值,则可考虑极值情况,即所丢的总分600分,均由低于60分的人数丢失,即其余人得分均为满分100分。
第三步,每个低于60分的人丢分高于40分,总丢分一定,如果每个人丢分越少,则这一部分总人数越多,假设每人按丢分41分,最多有600÷41≈14.6(人),结合选项,则低于60分的人最多为14人。
因此,选择D选项。
知识点:



