欢迎登录
- A. 3
- B. 4
- C. 5
- D. 6
-
视频解析
 免费试看
免费试看
-
解析
第一步,本题考查排列组合隔板法问题。
第二步,题目中出现每个党支部至少分a本,先给每个党支部分(a-1)本,构造隔板法模型,即先分给甲支部2本、分给乙支部1本、分给丙支部3本,则题目变成将11-(2+1+3)=5本手册分给甲、乙、丙三个党支部,每个党支部至少分一本,属于标准隔板法题型,应用公式 ,故有
,故有 种分配方式。
种分配方式。
因此,选择D选项。 -
考点
数量关系 数学运算 排列组合问题,方法技巧类
-
来源
2024年3月30日全国事业单位联考《职业能力倾向测验》(B类)考生回忆版第47题、2024年3月30日全国事业单位联考《职业能力倾向测验》(C类)考生回忆版第47题
- A. 16户
- B. 20户
- C. 22户
- D. 25户
-
解析
第一步,本题考查基础应用问题。
第二步,运用方程法求解。设贫困家庭有x户,则其他家庭有(110-x)户。由题意可得:3x+(110-x)×1=160,解得x=25。
因此,选择D选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
2020年8月1日河北省邯郸市涉县事业单位招聘考试(考生回忆版)第132题
- A. 16
- B. 20
- C. 22
- D. 25
-
解析
第一步,本题考查基础应用题。
第二步,设贫困家庭x户,则其他家庭(110-x)户,根据题目中条件可列式3x+(110-x)=160。
第三步,解得x=25。
因此,选择D选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
2023年4月22日辽宁省沈阳市浑南区社区工作者考试试卷(考生回忆版)第9题、2023年4月22日辽宁省沈阳市浑南区社区工作者考试试卷(考生回忆版)第9题
- A. 60
- B. 56
- C. 50
- D. 48
-
解析
第一步,本题考查基础应用题,用方程法解题。
第二步,设学生总数为x人,根据水果总数不变可列出等量关系式:2x+40=3x-20,解得x=60。
因此,选择A选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
2022年7月24日辽宁省阜新市细河区事业单位招聘考试(精选)(考生回忆版)第53题
- A. 16
- B. 20
- C. 22
- D. 25
-
解析
第一步,本题考查基础应用题,用方程法解题。
第二步,设贫困家庭有x户,则其他家庭有(110-x)户。由题意可得:3x+(110-x)×1=160,解得x=25。
因此,选择D选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
2015年0322广东公务员考试《行测》试题(乡镇)第43题
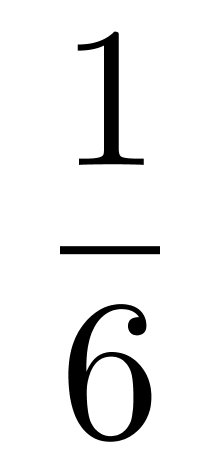 ;其次,第2人分得2百万和剩余部分的
;其次,第2人分得2百万和剩余部分的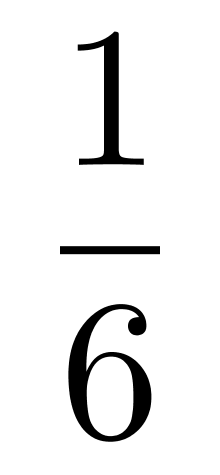 ;接下去第3人分得3百万和剩余部分的
;接下去第3人分得3百万和剩余部分的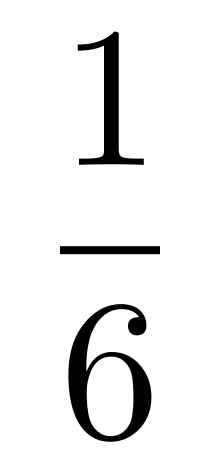 ;依次类推,最后剩余的部分全给了最后一个人。结果每人都得到了同样价值的宝藏。那么,该寻宝团队共有多少人?
;依次类推,最后剩余的部分全给了最后一个人。结果每人都得到了同样价值的宝藏。那么,该寻宝团队共有多少人? - A. 5
- B. 6
- C. 7
- D. 8
-
解析
解法一:
第一步,本题考查基础应用题。
第二步,设宝藏总量为x+100,则第一个人得到的宝藏为 ,还剩下宝藏的量为
,还剩下宝藏的量为 ;第2个人分得的宝藏为
;第2个人分得的宝藏为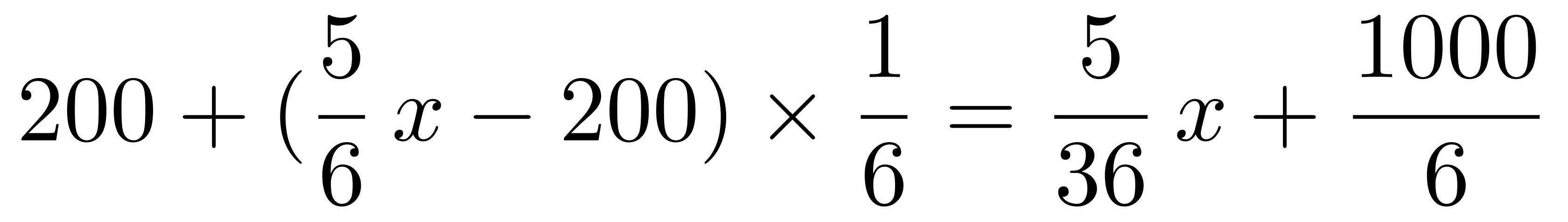 ,由于每人得到了同样价值的宝藏,即
,由于每人得到了同样价值的宝藏,即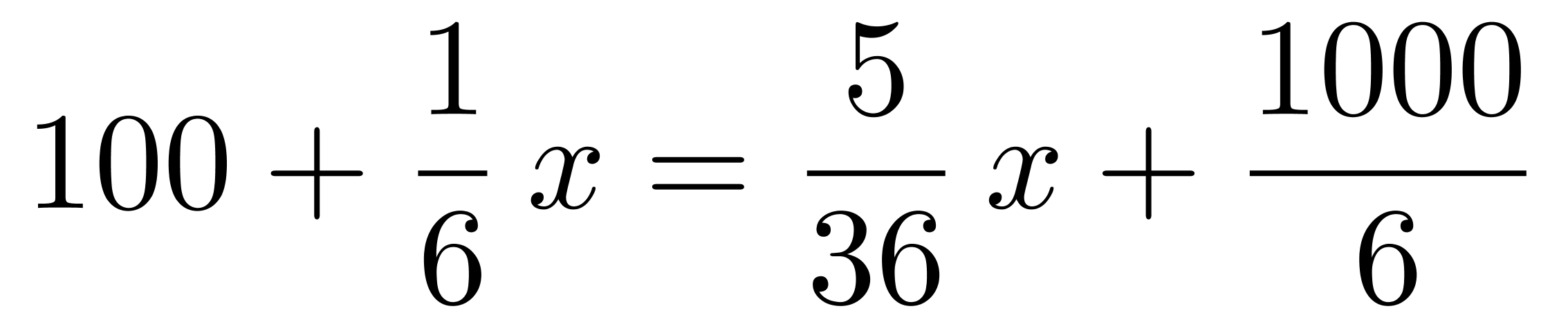 ,解得x=2400,所以第一个人得到的宝藏为
,解得x=2400,所以第一个人得到的宝藏为 ,总量为x+100=2500,故该寻宝团队共有2500÷500=5(人)。
,总量为x+100=2500,故该寻宝团队共有2500÷500=5(人)。
因此,选择A选项。
解法二:
第一步,本题考查基础应用题,用倒推法解题。
第二步,设该寻宝团队共有n个人,则第(n-1)人分得的宝藏为(n-1)百万+ 剩余。根据“最后剩余部分全给了最后一个人”,则最后一个人分得的宝藏为
剩余。根据“最后剩余部分全给了最后一个人”,则最后一个人分得的宝藏为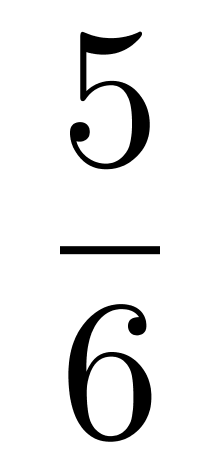 剩余。又根据规律第n人分得n百万后无剩余,即分得的宝藏为n百万,可列表如下所示:
剩余。又根据规律第n人分得n百万后无剩余,即分得的宝藏为n百万,可列表如下所示: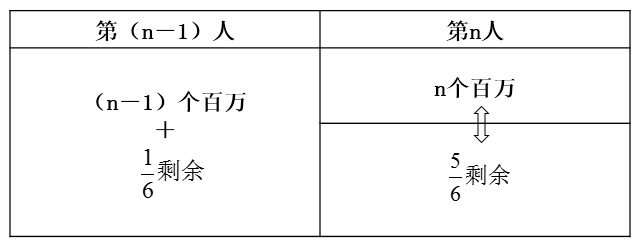
即n个百万=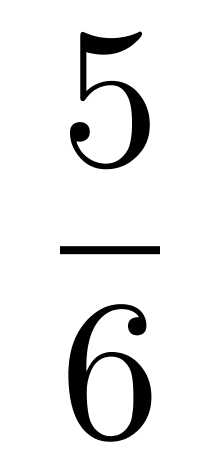 剩余,根据数字特性可知,n是5的倍数,结合选项,只有A选项满足。
剩余,根据数字特性可知,n是5的倍数,结合选项,只有A选项满足。
因此,选择A选项。 -
拓展
-
考点
数量关系 数学运算 基础应用题
-
来源
2018年1020重庆公务员考试《行测》试题(高速执法)第66题
- A. 20
- B. 15
- C. 18
- D. 12
-
解析
第一步,本题考查基础应用题。
第二步,设大班有x人,小班有y人,根据题意可列方程:5x+3y=135①,2x+2y=70②,解得x=15,y=20。
因此,选择A选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
2016年7月云南省事业单位统考《职测A类》试题(考生回忆版)第55题
- A. 28
- B. 36
- C. 54
- D. 78
-
解析
第一步,本题考查排列组合问题,属于方法技巧类。
第二步,根据隔板法的使用条件:将 n 个相同的元素分给 m 个组,每组至少得一个, 总的分配方法为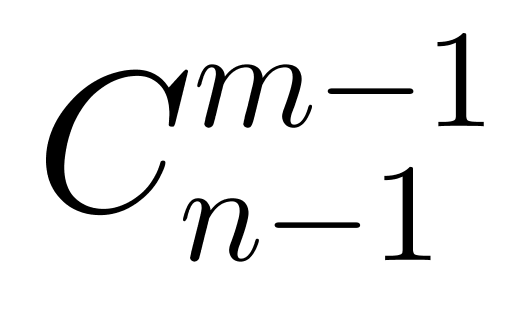 。由于每个下属至少分三项任务,可先给每个下属分2个任务,还剩余20-2×3=14(项)任务。再将14项任务分给三个下属,每人至少一个,就能保证每个下属至少三项任务,共有
。由于每个下属至少分三项任务,可先给每个下属分2个任务,还剩余20-2×3=14(项)任务。再将14项任务分给三个下属,每人至少一个,就能保证每个下属至少三项任务,共有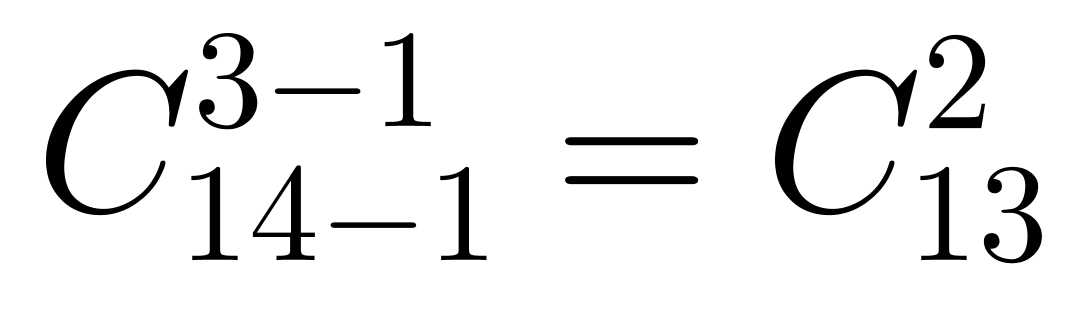 =78(种)分配方式。
=78(种)分配方式。
因此,选择D选项。 -
考点
数量关系 数学运算 排列组合问题
-
来源
2020年9月6日河南省洛阳市老城区事业单位考试(下午场)(考生回忆版)第119题
- A. 1653
- B. 3819
- C. 4018
- D. 5472
-
解析
第一步,本题考查的是基础应用题。
第二步,设A、B、C三个小区的人数分别为a、b、c,依题意得知: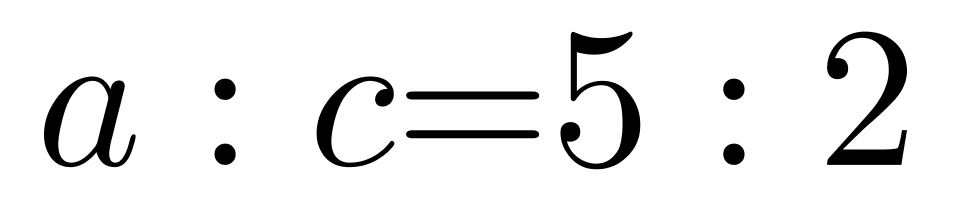 ,
, =4:3,三个小区的人数之比为:
=4:3,三个小区的人数之比为: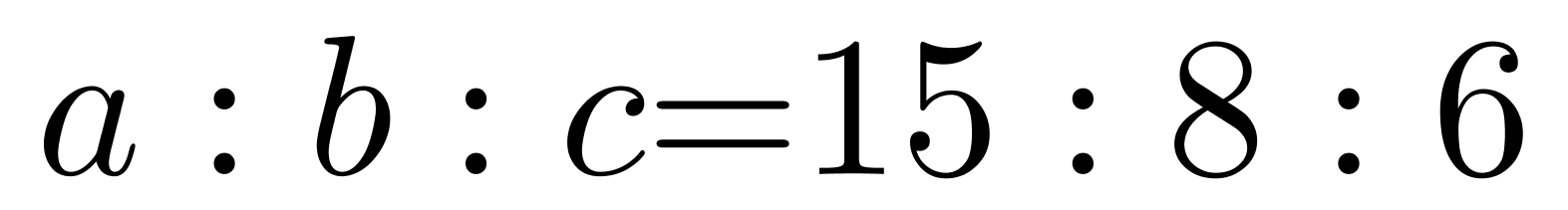 ,令C区的人数为
,令C区的人数为 ,则A、B小区的人数分别为
,则A、B小区的人数分别为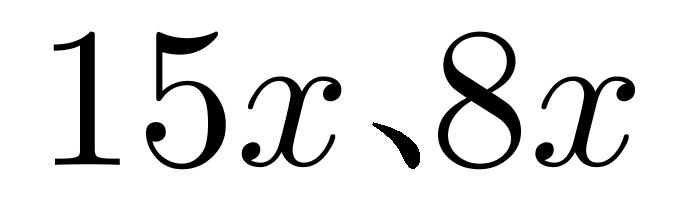 。三个小区的总人数为
。三个小区的总人数为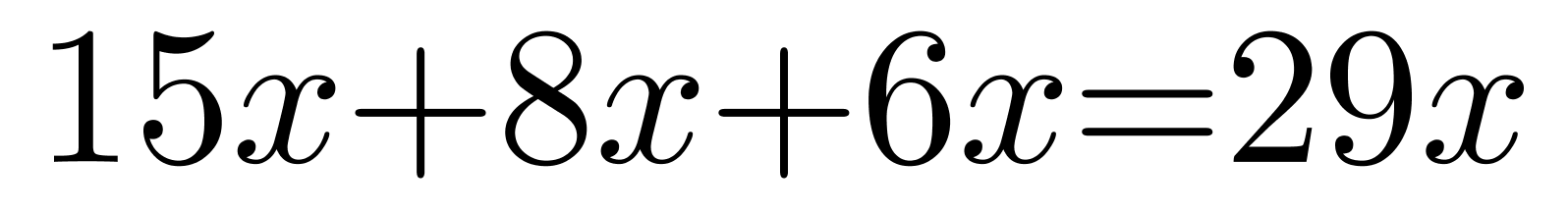 。因为总人数为500多人,所以总人数可能为:
。因为总人数为500多人,所以总人数可能为: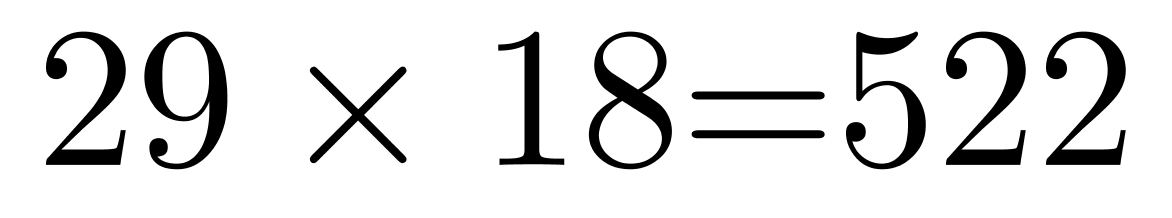 人、
人、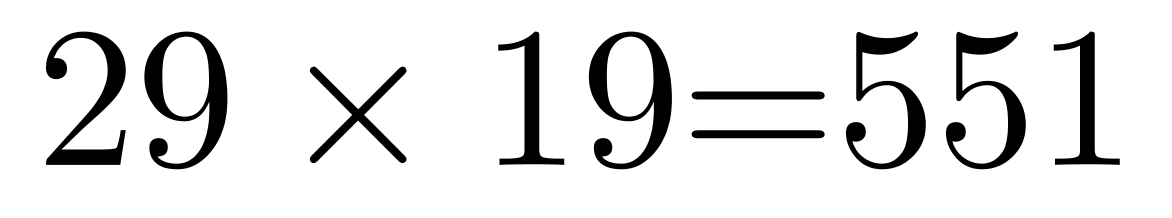 人、
人、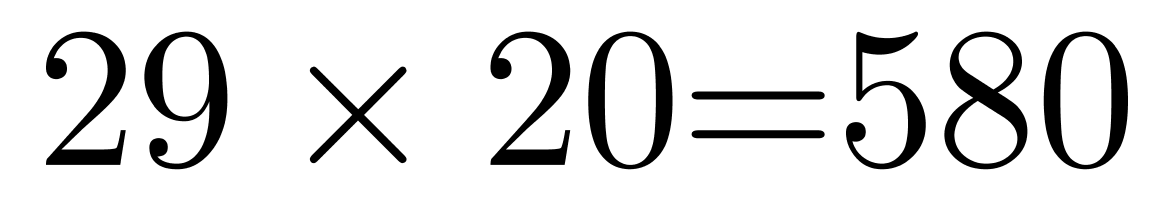 人。总抗原试剂为奇数支,且平均每人可以分得3支,所以三个小区的总人数必为奇数551人,则
人。总抗原试剂为奇数支,且平均每人可以分得3支,所以三个小区的总人数必为奇数551人,则 ,所以甲小区人数为
,所以甲小区人数为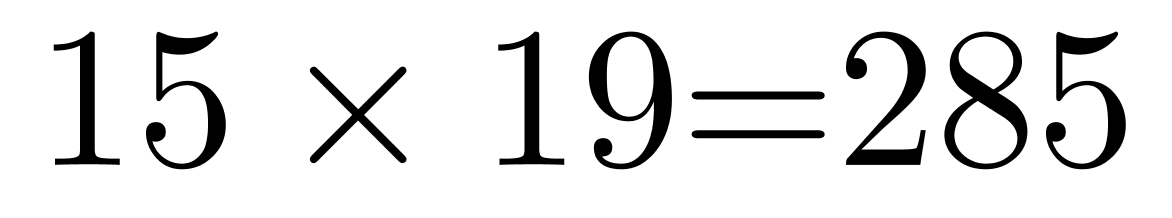 人,乙小区人数为
人,乙小区人数为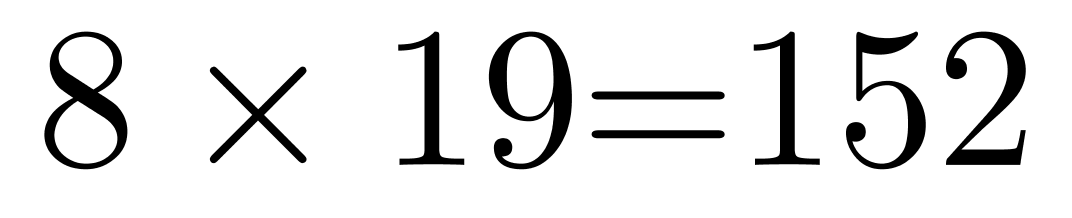 人,丙小区人数为
人,丙小区人数为 人。原有抗原检测试剂的总数为
人。原有抗原检测试剂的总数为 支。
支。
第三步,现要使得A、B、C三个小区每人分得的数量之比为4:3:2,且每人不得少于3支,则A、B、C三个小区每人最少分12支、9支、6支。需要的抗原检测试剂总量为: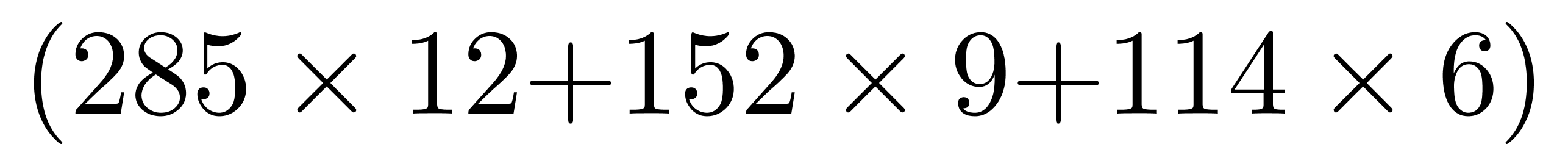 支,需要至少再购买:
支,需要至少再购买: ,此式计算量比较大,但观察选项,得知尾数不同,所以可以使用尾数法。经计算尾数为9,B选项符合。
,此式计算量比较大,但观察选项,得知尾数不同,所以可以使用尾数法。经计算尾数为9,B选项符合。
因此,选择B选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
模拟题
- A. 28
- B. 36
- C. 54
- D. 78
-
解析
第一步,本题考查排列组合问题,属于方法技巧类,用隔板法解题。
第二步,由于每个下属至少分3项任务,可先给每个下属分2项任务,还剩余20-2×3=14(项)任务。再将14项任务分给三个下属,每人至少一个,就能保证每个下属至少三项任务,共有 =
=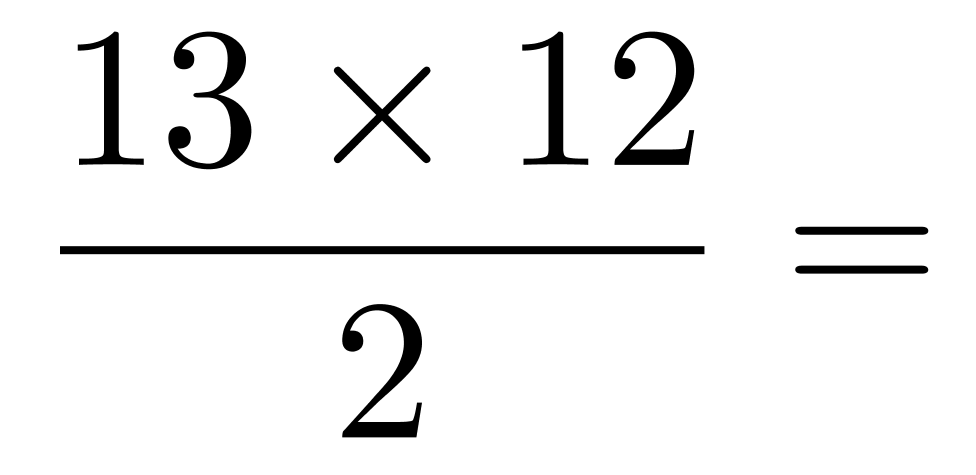 78(种)分配方式。
78(种)分配方式。
因此,选择D选项。 -
考点
数量关系 数学运算 排列组合问题,方法技巧类
-
来源
2019年0727江苏省宿迁市宿城区事业单位招聘专技岗试题(考生回忆版)第40题、2019年江苏省宿迁市属、宿城区事业单位试题《综合知识和能力素质》试题(考生回忆版)第40题
- A. 28
- B. 36
- C. 54
- D. 78
-
解析
第一步,本题考查排列组合问题,属于方法技巧类,用隔板法解题。
第二步,由于每个下属至少分3项任务,可先给每个下属分2项任务,还剩余20-2×3=14(项)任务。再将14项任务分给三个下属,每人至少一个,就能保证每个下属至少三项任务,共有 =
= 78(种)分配方式。
78(种)分配方式。
因此,选择D选项。 -
考点
数量关系 数学运算 排列组合问题,方法技巧类
-
来源
2019年0727江苏省宿迁市宿城区事业单位招聘专技岗真题第40题、2019年江苏省宿迁市属、宿城区事业单位试题《综合知识和能力素质》真题第40题
- A. 20
- B. 18
- C. 15
- D. 12
-
解析
第一步,本题考查基础应用题。
第二步,运用方程法求解。设大班x人,小班y人,根据题意可列方程:5x+3y=135①;2x+2y=70②。解得x=15,y=20。因此,小班有20个孩子。
因此,选择C选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
2021年4月17日河北省邢台市襄都区事业单位公共基础知识职业测试试题(考生回忆版)第93题
- A. 165
- B. 256
- C. 400
- D. 496
-
解析
第一步,本题考查排列组合问题,属于方法技巧类。
第二步,“每个下属至少分得3项任务”可以每个下属先分两项,而后每人至少分得一项。每个下属分两项,一共4×2=8(项),则12项任务分给4个下属,每个下属至少分得一项,代入隔板法公式: =165(种)。
=165(种)。
因此,选择A选项。 -
考点
数量关系 数学运算 排列组合问题,方法技巧类
-
来源
2018年0609天津市津南区静海区北辰区事业单位考试《职测》试题(考生回忆版)第13题
- A. 165
- B. 256
- C. 400
- D. 496
-
解析
第一步,本题考查排列组合问题,属于方法技巧类。
第二步,“每个下属至少分得3项任务”可以每个下属先分两项,而后每人至少分得一项。每个下属分两项,一共4×2=8(项),则12项任务分给4个下属,每个下属至少分得一项,代入隔板法公式: =165(种)。
=165(种)。
因此,选择A选项。 -
考点
数量关系 数学运算 排列组合问题,方法技巧类
-
来源
2018年0609天津市津南区静海区北辰区事业单位考试《职测》真题第13题
-
解析
低得分为0分,最高得分为50分,分数在0-50分之间,由于1分,2分,4分,7分,47分,49分都不可能出现,所以共有45种得分情况,至少:
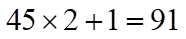 (人)。故本题答案为91。
(人)。故本题答案为91。 -
考点
中小学专业基础知识 数与代数 奥数 应用题
-
来源
2020年6月14日上海市宝山区小学数学试题第12题
-
解析
低得分为0分,最高得分为50分,分数在0-50分之间,由于1分,2分,4分,7分,47分,49分都不可能出现,所以共有45种得分情况,至少:
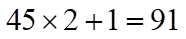 (人)。故本题答案为91。
(人)。故本题答案为91。 -
考点
中小学专业基础知识 数与代数 奥数 应用题
-
来源
2020年6月14日上海市宝山区小学数学真题第12题
- A. 1440万
- B. 1200万
- C. 1126万
- D. 1080万
-
解析
第一步,本题考查基础应用题,用数字特性法解题。
第二步,由题意可知,B子公司获得激励的员工中有27%的高管,也就是B子公司获得激励的员工× 是整数,则B子公司获得激励的员工人数是100的倍数,A子公司拟分配的总人数是B的两倍多,且是12+13=25的倍数,而总数是三百多人,那么B只能是100人,A子公司获得激励的员工最多是275人。那么普通员工人数最多为100-27+275×
是整数,则B子公司获得激励的员工人数是100的倍数,A子公司拟分配的总人数是B的两倍多,且是12+13=25的倍数,而总数是三百多人,那么B只能是100人,A子公司获得激励的员工最多是275人。那么普通员工人数最多为100-27+275×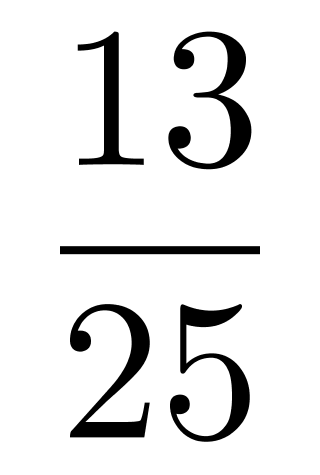 =216人,最多分得216×5=1080万股。
=216人,最多分得216×5=1080万股。
因此,选择D选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
模拟题
- A. 29 170
- B. 39 160
- C. 49 140
- D. 59 130
-
解析
第一步,本题考查基础应用题,用方程法解题。
第二步,设一类员工有x人,则另一类员工有(200-1-x)=(199-x)人。根据总设备可列方程:3x+(199-x)/2=198-1,解得x=39,另一类员工有199-39=160(人)。
因此,选择B选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
2018.9.15.青海省海东地区事业单位考试《职业能力倾向测验(C类)》真题第89题
- A. 29 170
- B. 39 160
- C. 49 140
- D. 59 130
-
解析
第一步,本题考查基础应用题,用方程法解题。
第二步,设一类员工有x人,则另一类员工有(200-1-x)=(199-x)人。根据总设备可列方程:3x+(199-x)/2=198-1,解得x=39,另一类员工有199-39=160(人)。
因此,选择B选项。 -
考点
数量关系 数学运算 基础应用题
-
来源
2018.9.15.青海省海东地区事业单位考试《职业能力倾向测验(C类)》试题(考生回忆版)第89题
- A. 13
- B. 14
- C. 15
- D. 16
-
解析
本题考查比赛问题。单循环比赛,比赛的场数为
 场,每场比赛胜者得1分、败者得0分,即每场比赛的总分数均为1分。设其余参赛队员得分均为x分,代入选项进行验证:
场,每场比赛胜者得1分、败者得0分,即每场比赛的总分数均为1分。设其余参赛队员得分均为x分,代入选项进行验证:
A选项,n=13,则比赛场数为 =78,总分数为78分,除去甲乙之外还有11人,可列式3+5+11x=78,解得x=
=78,总分数为78分,除去甲乙之外还有11人,可列式3+5+11x=78,解得x=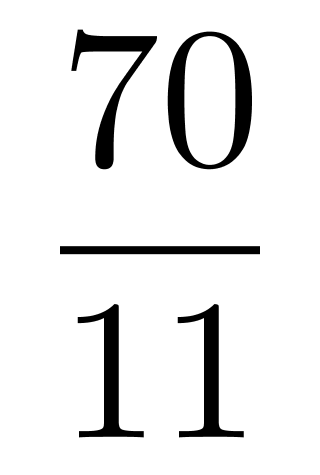 ,不是整数,排除;
,不是整数,排除;
B选项,n=14,则比赛场数为 =91,总分数为91分,除去甲乙之外还有12人,可列式3+5+12x=91,解得x=
=91,总分数为91分,除去甲乙之外还有12人,可列式3+5+12x=91,解得x= ,不是整数,排除;
,不是整数,排除;
C选项,n=15,则比赛场数为 =105,总分数为105分,除去甲乙之外还有13人,可列式3+5+13x=105,解得x=
=105,总分数为105分,除去甲乙之外还有13人,可列式3+5+13x=105,解得x=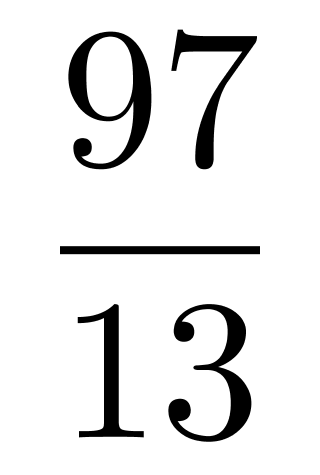 ,不是整数,排除;
,不是整数,排除;
D选项,n=16,则比赛场数为 =120,总分数为120分,除去甲乙之外还有14人,可列式3+5+14x=120,解得x=8,整数,满足。
=120,总分数为120分,除去甲乙之外还有14人,可列式3+5+14x=120,解得x=8,整数,满足。
故本题选D。 -
拓展
单循环赛制,是指所有参赛队在竞赛中均能相遇一次,n支队伍单循环比赛,场数为
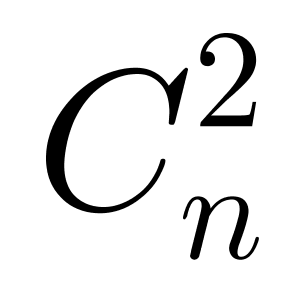 场。
场。 -
考点
数量关系 数学运算 比赛问题
-
来源
2021年4月3日陕西省西安市(幼小中)统考D类职业能力倾向测验试题第84题
联系方式:
咨询优惠
添加您的
专属公考咨询师

有协议班吗?
一课时多长时间?
手机可以观看吗?
课程可以反复学习吗?
可以下载吗?
课程包含图书吗?
错过直播有回放吗?
