
数学运算试题都是四选一的客观单项选择题,将选项直接代入进行验证,显然是一种准确、高效并且易于操作的重要方法。很多试题,正面求解相当困难,但结合选项来看却相当容易。“答案选项”永远是整个试题的有机组成部分,孤立的看题干而忽略选项是考生答题时最大的误区之一。
“代入排除法”广泛运用于多位数问题、不定方程问题、余数问题、年龄问题、周期问题、复杂行程问题、数字特性问题等。这种方法不仅可以单独使用达到一招致胜的效果,还可以与其他方法结合使用。
【例1】(2019 江苏A)一只密码箱的密码是一个三位数,满足:3个数字之和为19,十位上的数比个位上的数大2。若将百位上的数与个位上的数对调,得到一个新密码,且新密码数比原密码数大99,则原密码数是:
A. 397
B. 586
C. 675
D. 964
【答案】B
【解析】
第一步,本题考查多位数问题,用代入排除法解题。
第二步,根据十位上的数字比个位上的数字大2,发现四个选项都满足,根据百位上的数字与个位数字对调,新密码比原密码大99可得,只有B选项586对调后得到685,且685-586=99满足题意。
因此,选择B选项。
【例2】(2020 联考)某手机厂商生产甲、乙、丙三种机型,其中甲产量的2 倍与乙产量的5 倍之和等于丙产量的4 倍,丙产量与甲产量的2 倍之和等于乙产量的5倍。甲、乙、丙产量之比为:
A. 2 ∶ 1 ∶ 3
B. 2 ∶ 3 ∶ 4
C. 3 ∶ 2 ∶ 1
D. 3 ∶ 2 ∶ 4
【答案】D
【解析】
解法一:第一步,本题考查基础应用题,用代入排除法求解。
第二步,根据“甲产量的2倍与乙产量的5倍之和等于丙产量的4倍”可列出等量关系:2甲+5乙=4丙,根据奇偶特性可知,乙产量应该是偶数,优先代入C和D;C选项:2×3+5×2≠4×1,排除;D选项:2×3+5×2=4×4,暂且保留。根据“丙产量与甲产量的2倍之和等于乙产量的5倍”可列出等量关系:丙+2甲=5乙,D选项:4+2×3=5×2,满足此等量关系,D选项完全符合题意。
因此,选择D选项。
解法二:第一步,本题考查基础应用题。
第二步,设甲、乙、丙的产量分别为x,y,z。根据等量关系可列如下不定方程组:2x+5y=4z(1);z+2x=5y(2)。两式相加,得4x=3z,将此结果代入(2)式化简有2y=z,则x:y:z=3:2:4。
因此,选择D选项。
【例3】(2020上海)假设三颗小行星绕着一颗恒星运动,它们的运行轨道都是圆形,每条轨道的圆心都是该恒星。且三条轨道都在同一平面内。若这三颗小行星同向旋转,且绕轨道运行一周的时间分别是60年、84年、140年。现在三颗小行星和恒星在同一直线上且三颗小行星都在恒星的同侧,那么至少 年后他们再次在同一直线上且三颗小行星都在恒星的同侧。
A.210
B.315
C.420
D.630
【答案】A
【解析】第一步,本题考查循环周期问题,用代入排除法解题。
第二步,提问方式为"至少多少年",故从最小的选项A开始代入,210年后,周期为60年的小行星运行210÷60=3.5周,周期为84年的小行星运行210÷84=2.5周,周期为140年的小行星运行210÷140=1.5周,由于三颗小行星都运动到直径对应的另一端,因此处在恒星的同侧,满足题意。
因此,选择A选项。
【例4】(2020深圳) 王老师的日历如下图所示。他每天清晨撕下前一天的那页日历,某天下午,王老师将最近撕下的10页日历中的阿拉伯数字相加,算得总和为244。则当天该日历展示为( )日。
A.29
B.30
C.1
D.2
【答案】D
【解析】解法一:第一步,本题考查数列问题。
第二步,用代入排除法解题:代入A选项,当天日期是29日,撕下的10页是19—28,其和为(19+28)×10÷2≠244,排除;代入B选项,当天日期是30日,撕下的10页是20—29,其和为(20+29)×10÷2≠244,排除;代入C选项,当天日期是1日,撕下的10页是21—30,其和为(21+30)×10÷2≠244,或撕下的10页是22—31,其和为(22+31)×10÷2≠244,排除;代入D选项,当天日期是2日,撕下的10页是22—30、1,其和为(22+30)×9÷2+1≠244,或撕下的10页是23—31、1,其和为(23+31)×9÷2+1=244。
因此,选择D选项。
解法二:第一步,本题考查数列问题,用数字特性法解题。
第二步,若近10个日期是公差为1的等差数列,根据求和公式可知,前10项和为
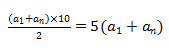
,应为5的倍数,244不是5的倍数。故前面10个数不完全连续,排除A、B、C选项。
因此,选择D选项。
代入排除法,不仅仅意味着把选项代入题干,还告诉我们在计算的过程中,应该一边计算一边比对答案选项,很可能算到一半,就可以得到正确的答案了。
祝大家攻坚克难、金榜题名!